There’s an old joke: “There are only 10 types of people in the world: those who understand binary, and those who don’t.” If you don’t get it now, hopefully you will after this post.
For most everyday tasks, we’ve been accustomed to using base-10, or “decimal” numerical system. Its what we’re taught from grade school and makes the most logical sense for humans. A quick recap on integer base-10 goes back to “ones”, “tens”, “hundreds”, and we say digits go from 0-9.
Let’s take a sample number 325. We say 325 is comprised of (3*100) + (2*10) + (5*1):
|--100's
||---10's
|||----1's
325
Or, an equivalent way of notation is:
|--10^2
||---10^1
|||----10^0
325
..in case you’ve forgotten algebra, I’ve linked Google Calculator above. For each number column, the digit represents that many 10^x. Like, 3 in the “hundreds column” is so because 10^2 is 100, and there’s 3 of them.
It’s called base-10, because the base number is 10.
In Binary, the base number is 2, a.k.a. base-2. In base-2, the digits go from 0-1, and each column is 2^x. So, if we take binary “1011”:
|---2^3
||----2^2
|||-----2^1
||||------2^0
1011
Reading the binary digits left to right, there’s 1 of (2^3) + 0 of (2^2) +1 of (2^1) + 1 of (2^0), OR (1*8) + (0*4) + (1*2) + (1*1) = 11 decimal.
While human brains process and store numbers in base-10, computer systems store data in binary, hence our discussion as a fundamental concept for software and embedded systems.
In nomenclature, each binary digit is called a “bit”. (binary 1011 is a 4 bit number). Data variables and CPU architectures are often referred to as number of bits. A 8-bit processor indicates that it natively processes data in 8-bit wide registers. A 16 bit data variable means it can hold up to 16 bits for that variable.
|-2^15
||--2^14
|| ...
|| |--2^1
|| ||---2^0
1010 1100 0011 1011
Writing out just 16 bits already starts to look like writing out credit card numbers. Imagine how long and tedious it gets to write out/read 32 bits, 64…
Luckily, there’s another numerical format: Hexadecimal, or “Hex”. Hex is base-16. There’s 16 digits. The first ten digits are 0-9. To avoid ambiguity, the eleventh through sixteenth digits are denoted A-F, so while binary digits go [0, 1] and decimal digits go [0, 1, 2, 3, 4, 5, 6, 7, 8, 9], hex digits go [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F].
Perhaps a table will help:
|decimal | binary | hex |
|--------|--------|-----|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
|--------|--------|-----|
From the table, each hex digit can be represented by a 4-bit binary value. That’s convenient in that you can group a binary representation into 4-bits and convert it to hex:
binary: 1010 1100 0011 1011
hex: A C 3 B
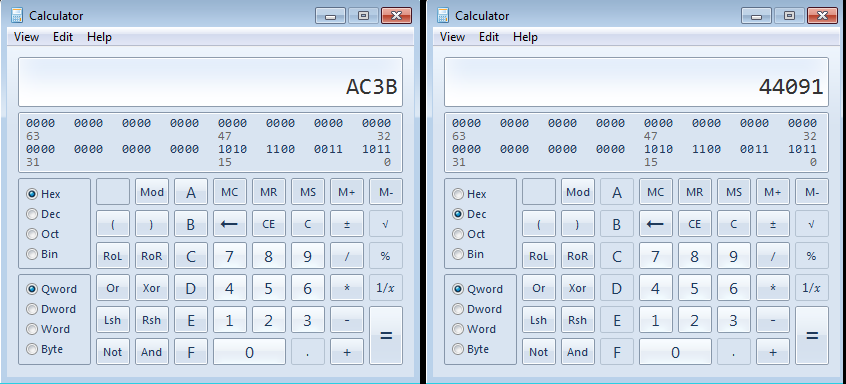
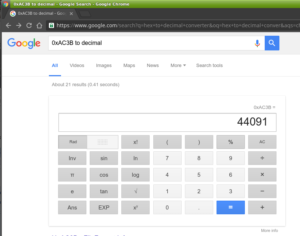
The binary value 1010110000111011 (commonly written as 0b1010110000111011 or 1010110000111011b) is equivalent to hex value AC3B (commonly written as 0xAC3B, or AC3Bh)
To convert to decimal, the value 0xAC3B can be viewed as:
|---16^3
||----16^2
|||-----16^1
||||------16^0
AC3B
where the number has
("A" *16^3) + ("C" *16^2) + (3 *16^1) + ("B" *16^0), or
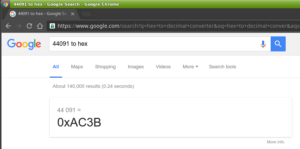
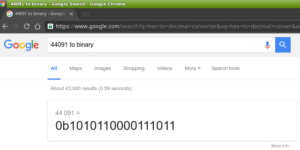
(10 *4096) + (12 * 256) + (3 * 16) + (11 * 1) == 44091 dec.
As with base-10 math, there are calculators available that aid in converting numerical representation.
On Windows, the “calc.exe” in programmer mode (View->Programmer) is handy:
You can also try the Google:
As a building block in software and embedded systems development, having a working knowledge of these three numerical systems are a prerequisite. There is another format, Octal, that’s base-8, that is usually also introduced in Computer Science. I think after going through binary and hex it isn’t to hard to figure out.